Results

A variety of different experiments were performed to determine the strengths and limitations of our system. Additional effort was focused on improving the squared error and handling target movement during the collection of the projections. Each of the following sections addresses the results of these efforts.

In all of the following images, any speckle noise is the result of artifacts during the conversion from MATLAB's image display to the GIF image file format used on these pages. A lack of available colors resident in the computer's graphics table, image scaling, and the file format itself produces these artifacts.

Case I

The first experiment was to determine the performance of our algorithm under three variables: number of projection angles, detector length, and number of detectors. The following reconstructed images represent a good sampling to demonstrate the strengths and weaknesses of the methodology. The squared error (SE) is also listed to give a quantitative comparison, along with the qualitative differences shown in the reconstructed images. The phantom image from which the reconstructions were made is shown at the top of Fig. 5.1. All reconstructed images for this experiment used the fftfilter.m in the backproj.m function.

Original Phantom Image

Number of Projection Angles = 45

Number of Detectors on the Detector Array

125 250 500

Detector
Array
Length

0.50

SE = 11092 SE = 16776 SE = 26032

1.00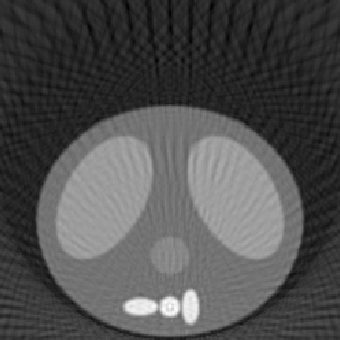

SE = 205.3 SE = 231.9 SE = 286.9

1.50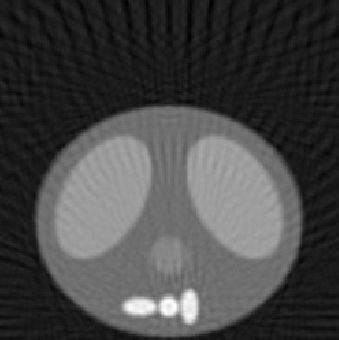

SE = 94.1 SE = 110.7 SE = 158.2

Number of Projection Angles = 135

Number of Detectors on the Detector Array

125 250 500

Detector
Array
Length

0.50

SE = 9810 SE = 13853 SE = 19743

1.00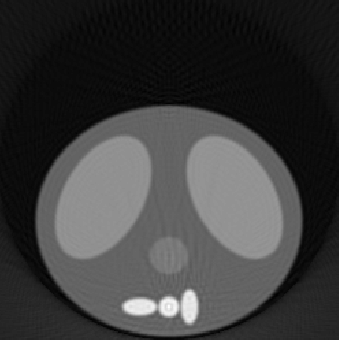

SE = 153.2 SE = 129.5 SE = 128.8

1.50

SE = 65.8 SE = 36.4 SE = 31.3

Number of Projection Angles = 250

Number of Detectors on the Detector Array

125 250 500

Detector
Array
Length

0.50

SE = 9589 SE = 13294 SE = 18480

1.00

SE = 151.2 SE = 121.3 SE = 109.5

1.50

SE = 65.5 SE = 32.9 SE = 18.5

Number of Projection Angles = 400

Number of Detectors on the Detector Array

125 250 500

Detector
Array
Length

0.50

SE = 9575 SE = 13122 SE = 17932

1.00

SE = 151.2 SE = 120.3 SE = 105.5

1.50

SE = 65.5 SE = 32.7 SE = 16.5

Figure 5.1 Images (originally 250x250 pixels) generated from the reconstruction
algorithm using the labeled number of projection angles, detector
length, and number of detectors. Squared error (SE) is also listed.

Case II

First inspection of the reconstructed images noted that some parts of the background have negative values. Although most of these values were small, this implies that a detector could receive a negative quantity of x-rays. Logically this does not make sense. The cause of the negative values comes from computational roundoff, and Gibb's phenomenon in the discrete Fourier transform filtering (fftfilter.m).

Removal of the negative values is reasonable since the difference between the background and any actual mass between the source and detectors is relatively large. An effort to remove the negative values should not disturb any real structure we want to observe. A simple program, zeroneg.m, was used to change all negative values to zero. The results are shown in Fig. 5.2.

Before After

Number of Angles = 250
Length of Detector = 1.5
No. of Detectors = 500

SE = 18.5 SE = 17.1

Number of Angles = 400
Length of Detector = 1.5
No. of Detectors = 500

SE = 16.5 SE = 16.0

Figure 5.2   A comparison of reconstructed images (originally 250x250 pixels)
   before and after changing all negative values to zero. Squared error
(SE) is also listed.

Case III

In this experiment, reconstructed images similar to Case I were obtained using the convolution back-projection algorithm (i.e., using convfilter.m instead of fftfilter.m).

Number of Projection Angles = 400

Number of Detectors on the Detector Array

125 250 500

Detector
Array
Length

0.50

SE = 7343 (9575) SE = 8376 (13122) SE = 10471 (17932)

1.0

SE = 39.59 (151.2) SE = 19.45 (120.3) SE = 11.47 (105.5)

1.50

SE = 60.2 (65.5) SE = 29.3 (32.7) SE = 15.26 (16.5)

Figure 5.3   Images (originally 250x250 pixels) generated from the convolution
   instead of the FFT based reconstruction algorithm using the labeled
   number of projection angles, detector length, and number of
   detectors. Squared error is also listed, along with the squared
error from Case I shown in ().

The above result shows an interesting difference in the two implementations of the filter. It can be seen that when the convolution based filter is used, the performance for detector length 1.0 is the best. This is possible because:

1. The sampling density of the projection is larger in this case than for a detector length of
1.5.
2. The non-zero portion of the thoracic cavity phantom is within the detector array.

The same is not observed, however, when the FFT based filter is used. This is due to the following difference in their implementation. In the FFT based implementation, the filtered projection is restricted to the same length as the projection. In the convolution based implementation, the filtered projection is longer than the projection. Due to this difference, the portions of the image that are not within the detector (the areas near the four corners of the image) are not reconstructed properly in the FFT based implementation but reconstructed well in the convolution based implementation. The top two corners are reconstructed well in both methods since most of the back-projection values for them will be zero. However, the bottom two corners contribute to most of the error in the FFT based implementation.

The following squared error images illustrate this.

FFT based filter Convolution based filter

Detector Array
Length = 1.0

Number of
Detectors = 500

Number of
projection
angles = 400

SE = 105.5 SE = 11.47

Figure 5.4 Images of squared error (pixel by pixel) after reconstruction.
Total squared error (SE) is also listed.

Case IV

In this experiment, we simulate the effect of shifts in the entire image and growth in specific regions like the lungs and heart. These changes occur during the process of determining the projections. In the specific simulation results shown, the shift, grow_lng or grow_hrt parameter used in project.m is modified halfway through the process of determining the projections.

Shift in Image Growth of Heart Growth of Lung

SE = 433.79 SE = 19.86 SE = 573.26

Figure 5.5    Reconstructed images with artifacts due to shifts in the image,
    or growth of regions, occurring halfway through the process of
   determining the projections. Number of projection angles = 400.
Number of detectors = 500. Detector length = 1.5. The shift and
growth parameters were changed after 200 projections were
obtained.

Shift in Image

with Correction

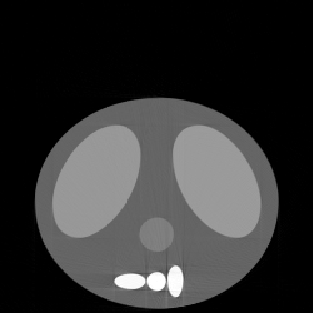SE = 36.88

Figure 5.6    Reconstructed image obtained after correction for shifts in the target
     during the collection of projections (using shiftfix.m). Note the artifacts
near the spinal column.

Case V

This section contains the results from our attempts at image enhancement. Six images were used and are listed below in Table 5.1. All reconstructed images for this experiment used the fftfilter.m in the backproj.m function. Each row corresponds to a different filter, described in the image enhancement section. The metric used to determine image quality was the total squared error between each reconstructed and filtered pixel and the corresponding original image pixels.

Table 5.1 IMAGE ENHANCEMENT SQUARED ERRORS

Filter	Image1	Image2	Image3	Shift	Heart	Lung
backproj.m	16.54	120.3	121.3	433.8	19.86	573.3
zeroneg.m	16.03	119.7	120.6	414.3	19.10	529.8
threshold	13.57	16.93	17.17	430.8	16.54	448.4
median (3X3)	13.47	16.74	16.70	424.9	16.51	447.2
wiener2 (3x3)	13.58	16.97	16.93	426.5	16.48	445.1
wavelet	28.19	30.32	30.56	429.8	31.37	454.4

Image1 generated using 400 Projection angles, array length 1.50, and 500 detectors.

Image2 generated using 400 Projection angles, array length 1.00, and 250 detectors.

Image3 generated using 250 Projection angles, array length 1.00, and 250 detectors.

Shift, Heart, and Lung are the images generated in Fig. 5.5 above.

Three things are immediately obvious from the above table. The first is that most of the squared error in images 2 and 3, which have low projection angles and detector array quantities compared to image 1, can be eliminated with the thresholding filter. Therefore, the biggest problem with smaller detector and projection amounts is the introduction of low valued artifacts outside the cavity. Secondly, we see that we were not able to improve much on reconstructed images where the lungs were expanded or the phantom shifted. Finally, we see that the edge thinning through the Haar wavelet transform actually increased the squared error. However, while the metric was increased, we see in the figures below that the edges are crisper.

Before After

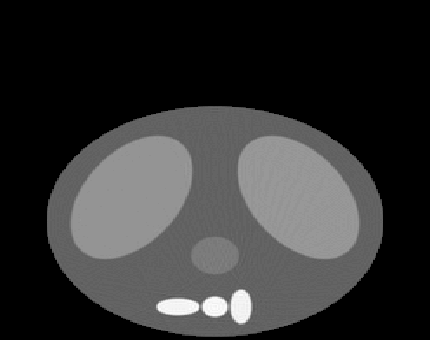Figure 5.7 Comparison of a reconstructed image after processing with our Haar
wavelet transform edge thinning algorithm.

Commentary on these results can be found in our conclusions section.

Final Results

After looking at the variety of outcomes from the above experiments, we applied our best algorithms to a single reconstruction. The final reconstructed image was generated using 400 projection angles, a length one detector, and 500 detectors on the array. We used the convolution back-projection to filter the projections. After the image was formed, post-processing algorithms included both zeroneg.m and median filtering. The final squared error was 9.61.

Original Thoracic Image Final Reconstruction

Image of Squared Error 3-D Image of Squared Error

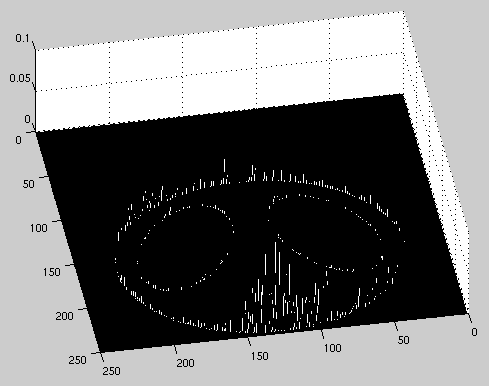Figure 5.8 The final reconstructed image (250x250) which had a squared error of 9.61,
along with plots of the error locations.